天気図上の移動距離から、低気圧や極大点の移動速度を求める問題がしばしば出題されます。
第51回実技1問2(1)③ 24時間のノットものさし
低気圧Aと低気圧Bの24時間の移動距離から、移動速度(ノット)を求める問題です。
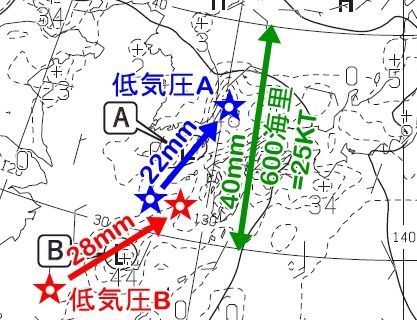
通常は、北緯30°~北緯40°の長さを測定してします。(40mm)
続いて、低気圧Aの移動距離の長さを測定します。(22mm)
移動速度=22/40×(600/24)=13.75ノットと算出します。
(正解は、13、14、15ノット)
低気圧Bは28mmなので
移動速度=28/40×(600/24)=17.5ノットと算出します。
(正解は、17、18、19ノット)
これを計算なしの作図だけで求める方法を提案します。
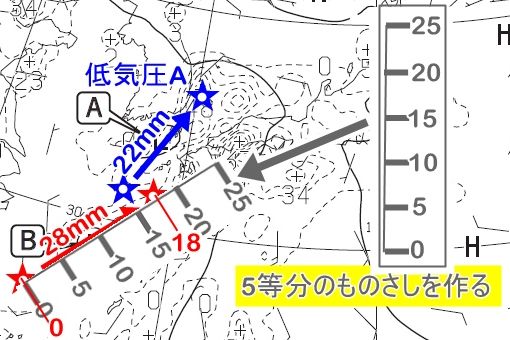
5等分のものさしを作って、直接ノット単位で読み取るのです。
5等分ものさしの作り方
24時間で移動した距離ですから、600海里のフルスケールが25ノットになります。
5等分して、5ノット単位のものさしを作ります。
平行線で分割するので、スケールを当てる角度は気にしなくていいです。
線を引きやすい角度にしましょう。
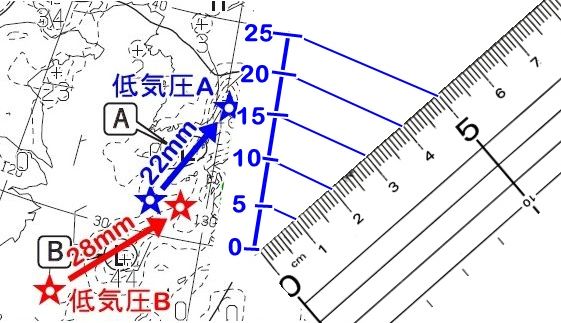
実際の作図状況を動画で示します。
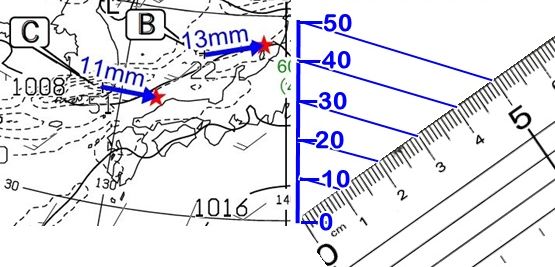
第50回実技1問2(5)③ 12時間のノットものさし
この問題は、降水極大点の移動速度を求めます。
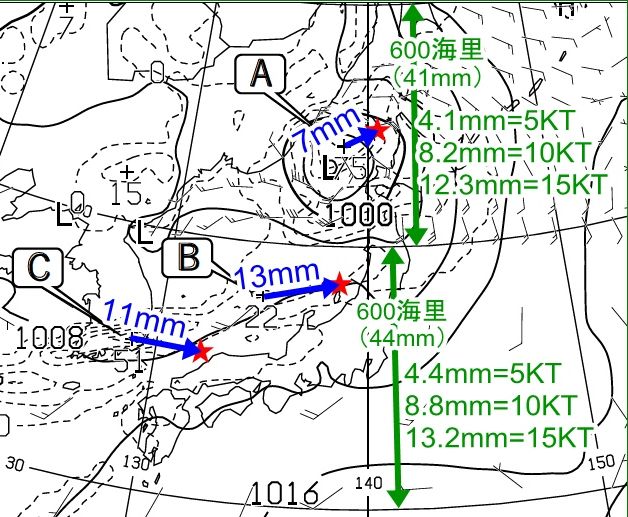
ノット専用ものさしの作り方は同じですが 12時間なのでフルスケール600海里は、50ノットになります。
上と同じように5等分して、50、40、30の目盛りを付けます。
これも動画を作りました。
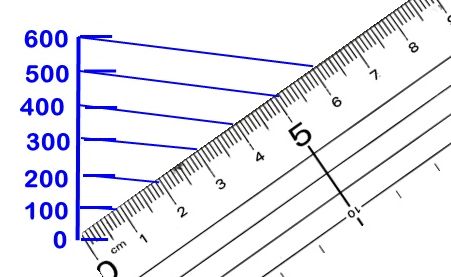
海里のものさし
移動速度ではなく、移動距離を海里で求める問題もあります。
その場合は、6等分してフルスケールを600海里にします。
600、500、400の順に目盛りを振れば、海里ものさしができます。
キロメートルものさし
移動距離を海里ではなく、キロメートルで求める問題もあります。
そんなときは、キロメートルものさしを作ることもできます。
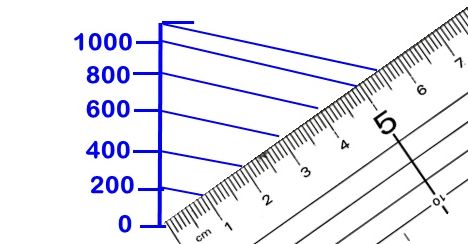
この場合は、フルスケールが1,110kmなので、
55mmを最上端に合わせると
50mmが1,000km
40mmが800m
30mmが600m
のスケールになります。
 手計算が苦手な人は、練習してみてください。
手計算が苦手な人は、練習してみてください。.
ちょっと慣れれば、案外便利ですよ。
.
三角定規の持ち込みが可能になったので、平行線が楽に引けます。
