予報精度の評価に関する問題は、毎回ほぼ1題は出題されているので、必ず確実に押さえておきたいところです。結構、範囲が狭いので、1ポイントゲットのチャンスポイントだと思います。
問題
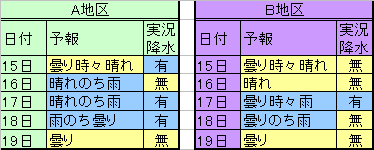
1)下の表はある期間のA地区とB地区の天気予報と 降水(1mm 以上)の有無を示したものである。
上の表に基づいて述べた次の文の正誤を答えよ。
1-1) この期間の捕捉率は,A地区のほうが高い。(正・誤)
1-2) この期間の降水ありの予報の適中率は,A地区のほうが高い。(正・誤)
1-3) この期間の降水の有無の空振り率は,A地区のほうが高い。(正・誤)
1-4) この期間の降水の有無の適中率はA地区のほうが高い。(正・誤)
2) 次の文の正誤を答えよ。
ある期間の気温予報の精度を評価するとき,その期間の予報値と実況値が完全に一致しなくても 2 乗平均平方根誤差(RMSE:Root Mean Square Error)が 0 となる場合がある。(正・誤)
3) 次の文の正誤を答えよ。
ある期間の気温予報の精度を評価するとき,その期間の予報値と実況値が完全に一致しなくても平均誤差(ME:Mean Error)が 0 となる場合がある。(正・誤)
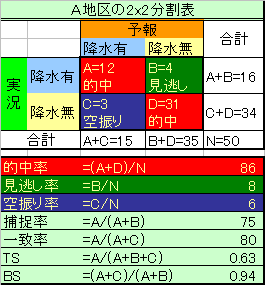
4) 下に示した、予報精度評価のための2×2分割表を見て、
次の数値を計算せよ。
(実際の学科試験では、数値を計算させる問題は出題されないが、計算ができることが前提です)
- A地区の降水の有無の的中率(%)。ただし少数点以下は切り捨てる。
- A地区の降水の有無の空振り率(%)。ただし少数点以下は切り捨てる。
- A地区の降水の有無の捕捉率(%)。ただし少数点以下は切り捨てる。
- A地区の降水の有無のスレットスコア(有効数字は少数以下2桁とする)
- A地区の降水の有無のバイアススコア(有効数字は少数以下2桁とする)
5) 気候値を当日の予報値とする気候値予報、前日の実況値を当日の予報値とした持続予報、および当日発表した予報値の精度検証の検証を行う。
下表は,ある月の 21 日と 22 日の早朝に発表した当日の最高気温の予報と,最高気温の気候値・実況値を示したものである。
この表をもとに,この 2 日間の気候値予報、持続予報、発表予報の 2 乗平均平方根誤差 (RMSE)を求めよ。
(実際の学科試験では、数値を計算させる問題は出題されないが、計算ができることが前提です)
| 20日 | 21日 | 22日 | |
| 予報(℃) | - | 28 | 27 |
| 気候値(℃) | - | 26 | 26 |
| 実況値(℃) | 27 | 28 | 25 |
6) 次の文の正誤を答えよ
ブライア・スコアは確率予報の検証に適した指標であり,降水確率予報の評価にも使われている。(正・誤)
7) 下表は降水の有無の予報と実況の2×2分割表である。この表を用いて降水の有無の予報精度の評価を行うときの指標に関する次の文の正誤を答えよ。
| 予報 | ||||
| 降水あり | 降水なし | 計 | ||
| 実況 | 降水あり | A | B | N1 |
| 降水なし | C | D | N2 | |
| 計 | M1 | M2 | N | |
7-1) 的中率とは全予報数に対する「降水あり」の適中回数割合であり,A/N で表される。(正・誤)
7-2) 捕捉率とは,実況「降水あり」の事例数に対する予報が的中した事例数の比であり,A/N1 で表される。(正・誤)
7-3) バイアススコアとは実況「降水あり」の事例数に対する予報「降水あり」の事例数の比であり,M1/N1 で表される。(正・誤)
7-4) スレットスコアとは適中率の計算において実況・予報ともに「降水なし」の事例を除外したものであり,A/(A+B+C) で表される。比較的まれな現象の予報精度の評価に適している。(正・誤)
7-5) スレットスコアは値が小さいほど予報精度が良い。(正・誤)
7-6) 見逃し率と空振り率は値が小さいほど予報精度が良い。(正・誤)
8) 次の文の正誤を答えよ
降水の有無の検証に用いるスレットスコアは,実況が 「 降水あり 」 となった場合のうち予報も 「 降水あり 」 であったものの割合である。(正・誤)
解答と解説
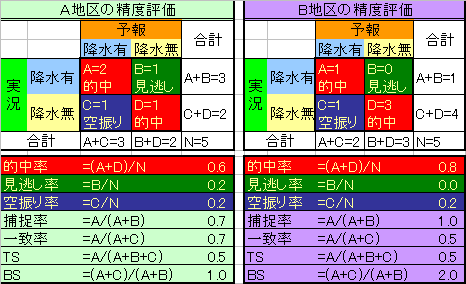
1)予報評価のための「2×2分割表」を作成して、的中率、見逃し率、空振り率、捕捉率、一致率、TS、BSを算出すると次の表になる。
「見逃し」とか「空振り」とか、正式な気象用語に、野球の言葉を使っているのが、ちょっと面白い。
式を解析すれば、その意味は自明だが、改めて文章に書いてみる。
的中率=(A+D)/N。雨が降る・降らないの予報が当たった。
最近の予報はさすがだねの確率。
見逃し率=B/N。
雨が降らないと言ったくせに、実際の雨を見逃したな。びしょぬれだよの確率。
空振り率=C/N。
雨の予報だったから傘を持っていったのに、空振りかよの確率。
狼少年率といっても良いかも。
見逃し率+空振り率=予報が外れた確率 これと的中率を足すと、当たり前だが1.0になる。
捕捉率=A/(A+B)。
実際に雨が降ったのを、どれだけ言い当てたかの確率。
一致率=A/(A+C)。
雨が振るって予想したなかで、実際にどれだけ降ったかの確率。
降水ありの的中率ともいう。
TS(スレット・スコア)=A/(A+B+C)。
発生が少ない現象を評価するときに使用する指数。当たって当たり前の評価指数Dを除いて計算する。
BS(バイアス・スコア)=(A+C)/(A+B)。
(雨降り予想)/(実際の雨)。
BSが大きいと狼少年になってしまう。
雨が降るぞ、降るぞと脅かすが、ちっとも降らないじゃないか、という具合。
ここまで整理すれば、答えは一目瞭然だ。
1-1) 誤。捕捉率はA=0.7<B=1.0だから、Bのほうが高い
1-2) 正。降水ありの予報の的中率は、一致率なのでA=0.7>B=0.5で、Aのほうが高い
1-3) 誤。空振り率は、A=0.2、B=0.2と等しい
1-4) 誤。的中率は、A=0.6<B=0.8だから、Bのほうが高い
2) 誤。
2 乗平均平方根誤差は、気温などの量的な予報値の精度評価に使われる。
予報値をFi、実況値をOiとするとき、平均誤差は、Σ(Fi-Oi)/N で計算され、正の偏差と負の偏差が相殺される。
これに対して、2 乗平均平方根誤差(RMSE)は、√{Σ(Fi-Oi)^2}/N で計算され、正と負の偏差が相殺されずに積算されるので、すべての予報値と実況値が一致しなければゼロにはならない。
3) 正。
上述の解説通り、単純な平均誤差は、正の偏差と、負の偏差が相殺して、ゼロになる場合がある。
4) 計算結果は次の通り。
5) 。
気候値とは、この場合平年値を指しているようだ。
計算値は以下の通り。
気候値予報:√[{(26-28)2+(26-25)2}/2]=√[{4+1}/2]=√2.5
持続予報:√[{(27-28)2+(28-25)2}/2]=√[{1+9}/2]=√5
発表予報:√[{(28-28)2+(27-25)2}/2]=√[{0+4}/2]=√2
6) 正。
ブライア・スコアとは、降水確率予報値をFi(0.0~1.0)、実況降水をOi(1または0、雨が降ったか降らなかったか)として、
BS={Σ(Fi-Oi)^2}/N の式で計算される。
BSが小さいほど精度が高く、完全な予報では0.0、最悪の予想では1.0となる。
ブライアスコアの計算例
| 日付 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 確率予報 | 0.1 | 0.6 | 0.4 | 0.9 | 0.7 | 0.4 | 0 | 0.6 | 0 | 0 |
| 実況降水 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
BS={(0.1-0)2+(0.6-1)2+(0.4-1)2+(0.9-1)2+(0.7-0)2+(0.4-0)2+(0.0-0)2+(0.6-0)2+(0.0-0)2+(0.0-0)2}/10
=1.35/10=0.135
7-1) 誤。
的中率とは全予報数に対する「降水あり」と「降水なし」の適中回数の割合であり,(A+D)/N で表される。
7-2) 正。
7-3) 正。
7-4) 正。
7-5) 誤。
値が大きいほど予報精度が良い。
7-6) 正。
いわば不的中率なので、小さいほうが良い。
8) 誤。
問題文の説明は「捕捉率」を示している。
スレット・スコアについては、上記1)の解説を参照のこと。