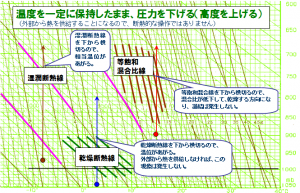
エマグラムの基本

エマグラムとは、Energy per unit mass diagram の意味で、ずばりこのグラフのことだ。


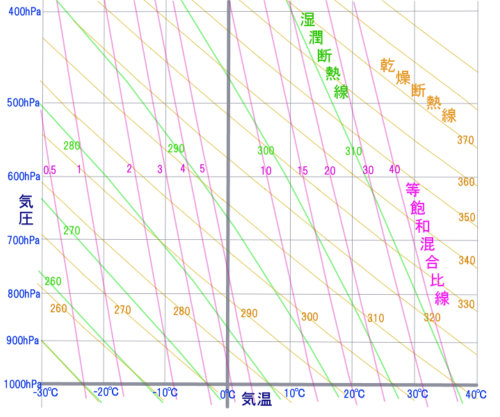
縦横が、気圧と気温の目盛になっているグラフ用紙に、3種類の線が引いてある。

一番寝ているのが茶色の「乾燥断熱線」

次が、グリーンの「湿潤断熱線」

一番立っているのが、「等飽和混合比線」

いずれの線も、左に傾いており、鉛直よりも右に傾いている線はない。

エマグラフの用紙に点を打ってみよう。

適当に、点Aをプロットしてみたのが、下の図である。


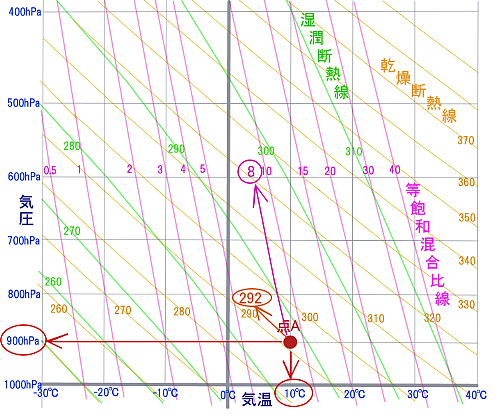
グラフ上に点Aを置いたが、これで何が分かるのだろうか。

1) 赤いラインを左にだどっていくと、現在の気圧が900ｈPaであることが分かる。

2) 赤いラインを下にたどっていくと、現在の気温が10℃(283K)であることが分かる。

3) 茶色のラインをたどっていくと、温位は、292Kである。

(数値はないが、290と300との比例関係で概数を読み取る)

4) ピンクのラインをたどっていくと、飽和混合比が8g/kgである。

(数値はないが、5と10との比例関係で概数を読み取る)

5) 〔気圧=900hPa〕と〔飽和混合比=8g/kg〕の情報から飽和水蒸気圧が計算できる。　

飽和水蒸気圧＝〔混合比(g/g)〕×〔空気圧(hPa)〕/0.622

=(8/1000)×900/0.622=11.6hPa

分かるのは、これだけだ。

飽和水蒸気圧は分かったが、実際にどれほどの水蒸気を含んでいるかは、分からない。

湿度（水蒸気）の情報が加われば、湿球温度、湿球温位も分かる。
その結果、相当温位も分かる。

しかし、この1点だけではそれは分からない。

湿度情報欲しいなぁ。

エマグラムのグラフ用紙で、まっすぐ上に上げるとは、どういう意味を持つのだろうか。

図示すると、こうなる。


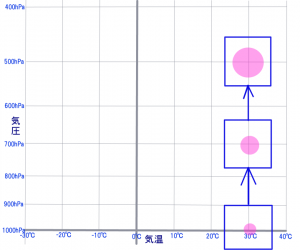
まったく張力を持たない、シャボン玉のような超薄皮の風船の中に、地上の空気を詰める。

地上の気温を30℃としよう。

この風船を、このまま持ち上げると、上空に昇るにしたがって気温が下がってしまうので、ここでは、30℃を保持する保温ボックスに入れることにする。この保温ボックスには、強力な温調装置がついていて、常に30℃に維持することが出来る。ただし、ボックスは密閉ではなく外圧と連通しているので、気圧は変化する。

地表を離れて上昇すると、外部の気温が下がるが、ここでは強力な温調機でボックスの内部を加熱しているので、温度は30℃と一定である。　過熱している分だけ、温位は上がってゆく。図示していないが、上昇する過程で何本もの「乾燥断熱線」をまたいでいる。「乾燥断熱線」は「等温位線」でもあるので、それを何本も下から上に超えていくということは、温位が上昇していることを示している。



さて、この箱に入った風船を700hPa（地上3000m)まで持ち上げたら、膨らんできた。当然、温度は保持されているので30℃のままだ。自然界なら上空に持ち上げると勝手に冷えてしまうから、自然界では見られない現象であることをよく理解しておこう。

さて、500hPa（地上5500m)まで持ち上げると、2倍に膨らんだ。



これは、気体の状態方程式で説明できる。

pv=nRT　というヤツだ。

風船の中の空気塊の量は変わらないし、温度も一定なので、nRTは一定で、pv=const、つまり圧力と体積は反比例すると言う意味になる。だから、圧力が1000hPaから500hPaへと半分に減圧すれば、体積は2倍になる。

この様子は、試験問題にしばしば出てくる「断熱的に持ち上げる」には当たらないので注意が必要だ。

エマグラムのグラフ上で、まっすぐ左に引っぱることは、気圧を変えないで、どんどん冷却する作用を意味している。

張力を持たないシャボン玉のような極薄の風船に空気を詰めて冷却した様子を図示するとこうなる。


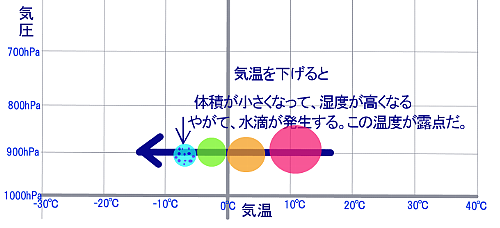
圧力が一定の場合は、気体の体積は絶対温度に比例する。

これも、気体の状態方程式で説明できる。

pv=nRT　というヤツだ。

pとnRが一定だから、v=Const×Tとなって、体積は絶対温度に比例するのだ。

上の図では、900hPaで、10℃の空気を冷却している。

10℃（283K）から-8℃(=265K)まで冷却したので、温度が6%下がった(265K/283K=94%)ので、体積も6%収縮する。（上の図の縮尺は大げさです）



風船の中の空気が、水蒸気を含まない乾燥空気であれば、温度が下がっても体積が小さくなるだけで他の変化は起きない。

しかし、水蒸気が含まれていると、だいぶ様子が変わってくる。

温度が下がると、空気中に存在できる水蒸気量が減る（飽和水蒸気圧の減少）ので、相対湿度が上昇するのだ。

さらに温度を下げてゆくと、空気中に存在できなくなった水蒸気が、水滴となって現れる。これを凝結という。

夏の暑い日に、氷水を入れたコップの周りに水滴がつく現象である。

凝結が始まるこの時の温度を「露点温度」という。



露点温度さえ分かってしまえば、こっちのもんだ。

何が「こっちのもの」なのかはともかく、湿度に関する情報が、圧倒的に多くなることは事実だ。

左に移動した時の様子を、乾燥断熱線と湿潤断熱線を対象に見てみると、こんな図が出来る。

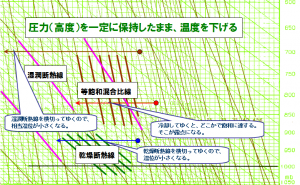
乾燥断熱線を何本もまたいで低いほうに動くので、温位は低下する。
同じように、湿潤断熱線もまたいで、低いほうに動くので、相当温位も低下する。
飽和混合比が低下するので、相対湿度が上がり、水分が存在すればいつかは飽和して凝結する。

この動きは、空気を外部から冷却することになるので、断熱的な現象ではないことに留意すること。
これは、しばしば試験に出るので重要だ。

勿論、右に動かしたら、温位も相当温位も上がるのは自明のことだ。

では、今度は、まっすぐ上に動かしたときのことを考えてみよう。

乾燥断熱線を何本もまたいで高いほうに動くので、温位は増加する。
同じように、湿潤断熱線もまたいで、高いほうに動くので、相当温位も増加する。
飽和混合比が増加するので、相対湿度が下がり、乾燥する方向である。

この動きは、空気を外部から加温することになるので、断熱的な現象ではないことに留意すること。

勿論、下に動かしたら、温位も相当温位も低下するのは自明のことだ。