エマグラムで直感的に分かることはたくさんあります。

エマグラムで遊んで、大気の状態を覚えましょう。

エマグラム専用用紙は、縦軸が気圧[hPa]の対数目盛（下が地表で上が上空）で、横軸が気温[℃]です。
図の中には、3本の斜めの線が引かれていて、45度くらいに寝ているのが乾燥断熱線、次が湿潤断熱線、70度くらいに立っているのが飽和混合比線です。

これらの線は、断熱過程での変化を表しています。

ここに、気圧=900hPa、気温=15℃の点を打ってみましょう。
図はこうなります。

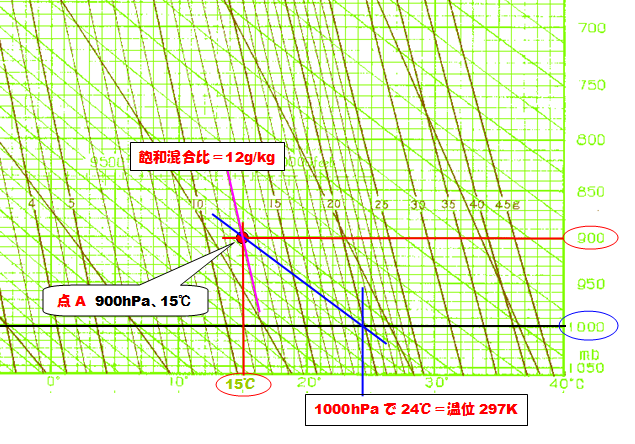
右の目盛から900hPaの水平線を引きます。
下の目盛から15℃の垂直線を立ち上げると、点Aの位置が自動的に決まります。

これによって、乾燥断熱を辿って1000hPaの温度を読むと24℃なので、273.15度を加えて絶対温度に換算すると、温位が297Kとなることが分かります。
（小数点以下は概算省略）

同時に、この点を通る等飽和混合比線から、飽和混合比が12g/kgであることも決まります。

つまり、気圧、気温、飽和混合比、温位のうち、2点が与えられれば、他の項目が自動的に決定されることになるのです。

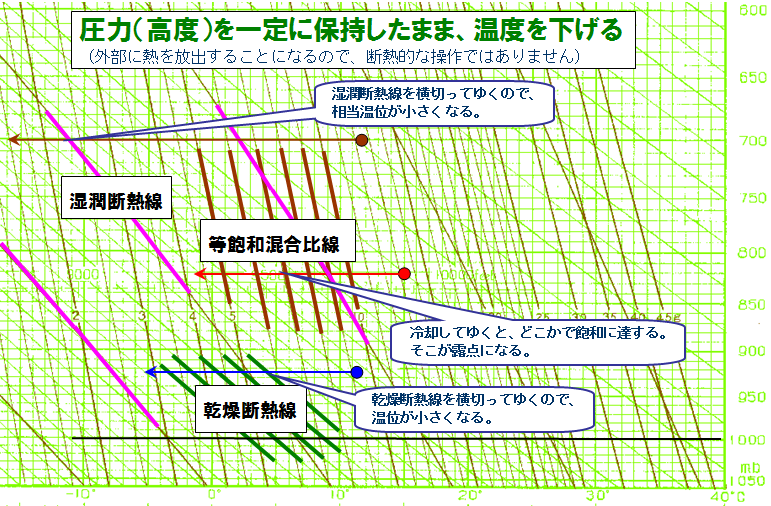
気圧を保持したまま温度を下げたらどうなるか

この現象は、例えば、地上（一定気圧）で空気塊を強制的に冷却するような状況に相当します。

実際の例としては、露点測定をイメージしてください。
地上で空気を冷却していくと、徐々に相対湿度が上昇して、やがて飽和に達して結露を生じます。
その温度が露点になります。

この様子をエマグラム上で表すと、水平に左に移動する動きになります。、

 

図で検証してみましょう。

 

露点測定の原理から、この動きによって相対湿度が上昇することが想像できますが、温位や相当温位はどのような変化をするでしょうか。

 

等飽和混合比線との関わり

最初に、赤い矢印線を見てみると、等飽和混合比線をまたいで、値が小さくなっているいます。
これは、飽和混合比がどんどん小さくなっていることを示しています。
つまり、空気中に保持する水蒸気量がどんどん少なくなるので、相対湿度は上昇します。

やがて最初に含んでいた蒸気量を下回ったところで飽和に達するので、凝結（結露）が始まります。
この時の温度が露点温度になるのです。

スタートの温度と露点温度との差が、湿数になります。

さらに温度を下げていくと、飽和混合比がさらに小さくなるので、空気中に存在できなくなり凝結した水滴がぼたぼたと落ちてくるはずです。
氷水を入れたコップの周囲に水滴が出来て、流れ落ちる現象ですね。

 

乾燥断熱線との関わり

次に青い矢印線に着目してみよう。
乾燥断熱線、言い換えれば等温位線をまたいでいるので、温位が小さくなっていることを示しています。

周囲から冷却するのだから、温位が小さくなるのは当然でしょう。

 

湿潤断熱線との関わり

最後に茶色の矢印線を見ると、湿潤断熱線つまり相当温位線をまたいで相当温位が小さくなっています。

 

 

 

温度を維持したまま気圧を下げたらどうなるか

エマグラム上で、まっすぐ上に移動する動きになります。
減圧しながら加熱する動きなので、自然界では再現しにくい状況です。

図示するとこうなります。

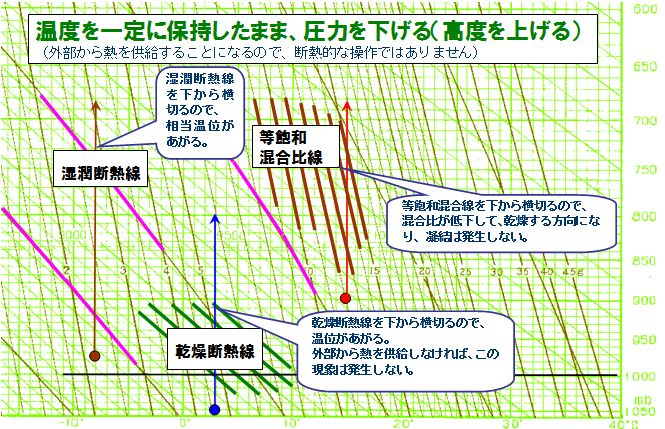
まず、赤い矢印を見ると、等飽和混合比線をまたいで、飽和混合比が大きくなる方向に動いているので、水蒸気量が変わらないとすれば、乾燥する動きになり凝結は発生しません。

次に、青い矢印に注目してみると、乾燥断熱線をまたいで、温位が大きくなる方向に動いていますね。
温位が大きくなるということは、同じ気圧なら温度が高くなることです。

 

1000hPaで気温5℃の空気塊を断熱変化で乾燥断熱線に沿って高度を上げると900hPaでは
・・・気温は4℃くらいに低下します。

でも、青の矢印のように真っ直ぐに上昇させると5℃のまま、あれ？
ちょっと変だぞ。

青の矢印では、断熱変化のときよりも気温が上がっている！
何故だろう？

実は、空気塊が周りから熱をもらいながら上昇したからなのです。
1℃分の熱をもらうことができたのです。

これを等温変化と言います。

 

空気塊の上昇スピードに合わせながら適切に熱を供給しないといつも気温一定の状態にはできないので、自然界では起こりにくい現象です。

 

断熱的に上昇させたらどうなる

では、加熱や冷却なしに空気塊を上空に持ち上げたらどうなるか。
これが、おなじみの断熱的な操作で、最初は乾燥断熱線に沿って上がることになるのです。

解説するための参考図を示します。

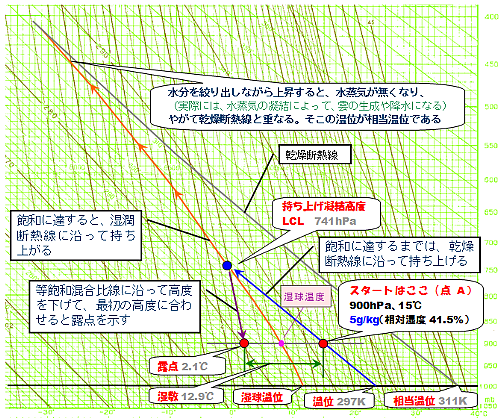
最初に設定した、点A（900hPaで15℃）をスタートしましょう。

この点の温位は297Kで、飽和混合比は12g/kgであることが決まっていることは、最初に説明したとおりです。

ここで、今後の説明のために、現在の混合比を仮に5g/kgと設定しておくことにします。
飽和混合比が12g/kgなので、相対湿度は5/12=41.7%になりますね。

 

飽和するまでは乾燥断熱線

ここから断熱的に空気を上空に持ち上げるためには垂直な線を引いてはいけまえん。
青い色で示した乾燥断熱線に沿って左上の方向に上がってゆくのです。

気圧の減少と共に温度は下がってゆきます。
当たり前の現象が確認できました。

スタート点の飽和混合比は12g/kgだったが、等飽和混合比線をまたいで進んでいくと、値がどんどん小さくなってゆきます。

仮に設定した5g/kgの等飽和混合比線と交差したところで、飽和に達します。

青い丸で示した点が、持ち上げ凝結高度（LCL)です。
ここで等飽和混合比線と900hPaの交点を見ると、露点温度（2.1℃）が分かりますね。

露点温度（2.1℃）と現在の温度（15℃）との差（12.9℃）を、湿数と言います。

ついでに、LCLから湿潤断熱線に沿って1000hPaまで落とすと、湿球温位が分かるのです。

図示していませんが、元の気圧（900hPa）との交点が湿球温度になります。

エマグラムの操作でいろいろな指標が見えてきますね。

 

飽和に達したら湿潤断熱線

さて、青い線で示した乾燥断熱線に沿って空気を持ち上げましたが、飽和に達すると挙動が変わってきます。

ここから上は、オレンジ色で示した湿潤断熱線に沿って上昇を続けることになります。

なぜかというと、飽和してからさらに温度が下がるので、空気中の水蒸気が凝結して水滴に変わるので潜熱を発することになり、青い線のまま進むことが出来なくなるのです。

 

だから、どうしても、オレンジ色の線に乗り換えなければならないのです。

オレンジ色の線を良く見てみると、乾燥断熱線をまたいで大きい数字になっています、つまり温位が上がっているのです。
何故温位が上がるかといえば、凝結熱（潜熱）が発生するからです。

熱帯で水蒸気がどんどん蒸発すると、上空に暖気核ができますが、それはこんな理由からなのです。
暖気核が、やがて台風を育てることにもつながります。

水蒸気をどんどん凝結させながら、つまり水蒸気を絞り出して雲や霧や雨を作りながら、温位を上げているのです。

 

上空では湿潤断熱線と乾燥断熱線が重なる

しかし、保持している水蒸気には限りがあり、雲を作りながら（あるいは雨を降らせながら）上昇してゆけば、空気はだんだん乾燥状態に近づいてゆきます。
やがて、水蒸気を全部吐き出してしまったら、もうそれ以上温位が上がることはありません。

ふと見ると、オレンジ色の湿潤断熱線は、グレーの乾燥断熱線と重なっていることに気が付きます。
重なったところから、グレーで示した乾燥断熱線に沿って1000hPaまで下げてみると、311Kですね。
これが、最初に与えられた「点A」（900hPa、15℃、混合比5g/kg）の相当温位を示しているのです。

 

この作図で操作したことを振り返れば、相当温位とは、当初保持していた水蒸気をすべて吐き出して持っていた潜熱を温位に変化させて上昇させた後に到達した温位であることが、図から読み取れます。
相当温位が温位よりも右側にあることが明白であり、温位(θ)<相当温位(θe)であることも必然的に頭に残リますね。
是非、残してください。

 

 

文章で読むと、すごくごちゃごちゃしていますが、じっくりと線をたどってみれば、簡単に分かるはずです。

エマグラムを嫌わず、頼りになるツールとして活用してください。

 

 

例題：自分で考えてください。