終端速度は rの2乗か、ルートrか
KSさん(2013/06/25)からの質問です。
降水過程での雨滴の落下速度に関連した質問です。
財目かおり氏著の「気象予報士かんたん合格ノ－ト」のp27の解説では、導入式が、
抵抗力Fが F＝6πηrV （η：粘度）
でmgと釣り合うとして
mg＝6πηrV となり
ここでも m＝（4/3）πr3ρw を代入して
V＝（2ρwr2g）/（9η）
という式を導いています。
さらに解説では、「終端速度の式からは、速度は半径の2乗に比例する」と記載されています。
これから、前問を考えると雨滴半径が2倍になれば速度は4倍になり正解は[5]になってしまいます。
これは間違いなのですか。
結論から言うと、同じ雨粒の落下速度と言っても、粒の大きさで挙動が異なることが誤解の原因です。
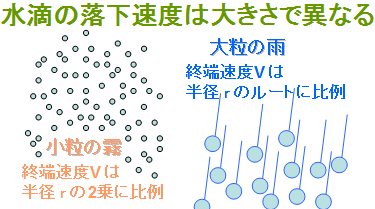物質が落下するときに邪魔になる因子は二つあります。
一つは空気の粘性です。 水滴が0.1mm以下の場合に有効です。
二つ目は、慣性力です。 水滴が0.7mm~2mm程度で有効です。
空気の粘性は、風の影響と同じ意味合いです。
落下速度が遅いときには風が大きく作用します。たとえば、 鳥の羽毛やタンポポの綿毛などを落下させるときには、 空気の粘性によってふわふわ浮いています。実際の水滴で言えば、粒子が細かい霧やもや等の微粒子はいつまでも空中に浮遊して、 僅かなそよ風でも流れてしまいますから、 風の影響を受けやすいと言えます。
一方、パチンコの玉や砲丸投げの球を落下させるときには空気の粘性（風の影響）なん か無視してストーンと落下します。 同様に粒子径が大きい夕立のような激しい雨では、 少々の風など関係なくまっすぐに落ちてしまいます。
問題になった二つの式は、この違いを表しています。
前問では、「直径1mm程度の雨滴」 と表現しており、 大粒であるから空気の粘性を無視して慣性力の抵抗だけに着目した 結果、「落下速度は水滴の半径のルートに比例する」 という結論に至っています。
一方、財目かおりさんの mg＝6πηrV の考え方は、空気の粘性だけに着目して、 慣性力を無視した式です。おそらく、前提条件として、「r またはV が小さいときには」という条件がついているはずです。
ですから雨滴が
・0.1mmより小さい場合の落下速度は「 半径の2乗に比例」して、
・0.7mm以上では「 半径のルートに比例」する。
・0.1~0.7mm辺りでは、 両者の中間の関係になるのです。
・2mm以上になると、 水滴がゆがんで球形ではなくなるので単純計算は出来ません。
・ 更に大きくなると二つに分裂して、 8mmを超える雨滴は地上では観察されていません。
一言で雨粒とか水滴と言っても、 粒子の大きさによって違う挙動を示します。
微粒子の場合は、V∝r^2(rの2乗に比例する) であり、 大粒の場合は、V∝√r(rのルートに比例する) になります。
これを覚えるために、語呂合わせの呪文『小粒の雨には自浄作用』を考案しました。
0.1mm～0. 7mmの粒子はこの中間の性質を持つため計算が複雑になるので、 気象予報士の試験には出ないと思います。
この手の問題では、必ず、微粒子であるとか、 直径1mm付近とか、粒径を指定する言葉が付くはずですから、 それを見逃さないように注意しましょう。
小倉義光著「一般気象学【第2版】」をお持ちでしたら、 86ページの表4.1をご覧ください。
直径と終端速度の例が掲載されています。
これらの数字で計算してみると、 微粒子では終端速度が半径rの2乗に比例しており、 粒子径が大きくなると√rに比例している様子が伺えます。