- このトピックには14件の返信、1人の参加者があり、最後に
により1年、 10ヶ月前に更新されました。
-
投稿
-
-
過去問に取り組んでるのですが、どうしても解けない問題があって不可解なので、先輩方、教えてください！
その１
平成28年第1回《46回》問２ ２段落目途中以降
飽和した空気塊の上昇に伴って凝結した水分が空気塊から離れて落下すると、空気塊の相当温位は低下する。
→ 回答×
■『凝結した水分が空気塊から離れて落下する』・・・これは雨になって降ると考えることだと思うのですが、そうすると、そこの空気塊は水蒸気量が減少するわけで、極端な話、乾燥するまで雨が降れば、相当温位は低下するのではないのですか？その２
同じく、平成28年第1回《46回》問４ (d)
水滴同士が衝突し、併合して成長する過程では、水滴の半径の単位時間あたりの増加『率』は一般に水滴が小さいときには大きいが、水滴が成長するにしたがって小さくなる。
→ 回答×
■増加速度なら理解できますが、増加率なので問題文通りでは？？？
例えば、半径１の水滴に別の水滴１が併合すれば増加率は大ですが、成長して半径20の水滴に半径19の水滴が併合してもそれ以上にはなりえず、成長するにしたがって小さくなる・・・のではないのしょうか？仮に上の例えで、半径20の水滴にそれより大きな半径30の水滴が併合する事がある！というのであれば、半径30から見れば、より小さい半径の水滴と併合している訳で・・・理解できないのです。
助けてください！
-
こまちさん
相当温位はある空気塊が全て水蒸気を凝結させた時の温位ですから、同じ空気塊である限り、途中の凝結の程度により変わるものではありません。
また、衝突による併合過程では大きな雨粒が、沢山ある小さな雨粒を一気に併合しますので、小さな雨粒よりも増加率は高いです。
-
ご返事がないところを見ると、まだ釈然とされてなさそうです。テリーさんのコメントの通りですが、ご自身の見方を見直すやり方をされてみてはいかがでしょうか。
相当温位の件については、例えば温位が同じで水蒸気量が異なるようなふたつの空気塊で比較すれば、確かに水蒸気量が少ない方が相当温位は低くなります。ただ、ここではひとつの空気塊を断熱変化させて凝結させているだけです。こまちさんの言葉を借りれば、「その空気塊を乾燥するまで雨を降らせた」ときの温位がその空気塊の相当温位なので、その空気塊自身の相当温位は変化しないということになります。
二つめについては、「半径20の水滴に半径19の水滴が併合してもそれ以上にはなりえず」との記載が気になりました。ここでの増加率は、併合する水滴の半径の変化は関係なく、シンプルに併合された後の水滴の半径の時間当たりの増える割合を指しています（こまきさんが増加速度と解釈されているものが相当しそう）。よって、半径が大きく速度も大きい水滴の方が、当然ながら単位時間あたりに併合できる量が多くなり、半径の成長？も大きくなります。
-
ありがとうございます
私、ひねくれてる訳ではないのですが、問題文を読み取る力がないのでしょうか？
気象予報士の試験問題はどうも、日本語の言い回しに囚われる感があり、理解しにくいものが多い気がします。
本質はそこなの？っていう問題が多い感を受けます。仰せの通り釈然としないままですが、試験を出す側に対峙しても仕方がないので理解していきます。
いずれにしても、ご丁寧にご回答いただきましたお二方には感謝です。
誠にありがとうございます。 -
その１は、状況説明の読解はこまちさんの解釈で正しいのですが、相当温位を温位と勘違いされたのではと思います。両者の定義を再確認されたらいいと思います。
その２は、大事な問題を含んでおり、こまちさんのおっしゃる通り、増加速度と増加率とは異なる概念です。一般に増加速度（dr/dt）が時間とともに大きくなるからといって増加率(r2/r1)が時間とともに大きくなるとは限りません。すなわち、単位時間あたりに併合できる量が多くなるからと言って半径の増加率が大きくなるとは限りません。ただ、この設問の”併合過程”の場合(dr/dtがｒの二乗に比例する場合)は、増加率も大きくなるというのが正解となります。仮に、dr/dtがｒの０.5乗に比例する場合は、増加速度は時間とともに大きくなりますが増加率は小さくなります。 -
①かねけんさん、ありがとうございます
飽和した空気塊の上昇に伴って凝結した水分が空気塊から離れて「落下する」・・・
仮に850hpa面に仮にΘe:300Kの空気塊があって、雨となって「落下」すれば、この空気塊の含有水蒸気量は減るので、Θeが300Kから下がるのではないのですか？・・・だって、空気塊に含まれてた水蒸気は地表面に落ちてしまってる・・・と解釈しました。
水滴になって「落下してない」なら理解できますが、もはや空気塊の性質が変化してるのではないでしょうか。
当然ながら温位としては空気塊の気温低下を伴うので変化しているのは理解できますが。
もはや日本語の問題になってますが(泣)・・・②ていねんまじかさん、ありがとうございます。
当然ながら単位時間あたりに併合できる量が多くなり、半径の成長？も大きくなります。
数字は大きさとして・・・
１＋１＝２ 増加率１００％ 【Ａ】
２＋２＝４ 増加率１００％ 【Ｂ】
・・・
１００＋１００＝２００ 増加率１００％ 【Ｃ】
１００＋１００未満＝２００未満 増加率１００％未満 【Ｄ】
１００＋（一気に１Ｘ１００以上） 増加率１００％超 【Ｅ】そうすると、初めのうちは【Ａ】とか【Ｂ】のパターンだけど、大きくなってくると私は【Ｄ】のパターンだと思ってたのでした。
だけど、大きな粒になると、小さい雨粒を一気に併合できるから【Ｅ】のパターンになるということですね。
これは理解できました。・・・が、しかし本当に（一気に１Ｘ１００以上）をキャッチできるのですか？
仮に（便宜的に）直径１の粒が横一列に同間隔（仮に間隔を１）で１００粒降ったとすれば幅２００になります。つたないイメージですが・・・
↓１↓（１）↓１↓（１）↓１↓（１）↓１↓・・・この間に雨粒は幅２００に１００粒
↓１↓（１）↓１↓（１）↓１↓（１）↓１↓・・・増加率１００％しかし、同じ条件で幅１００の雨粒が降った場合、併合できるのは幅１００のぶんなので５０粒しか併合できません。
↓—————–１００—————–↓ 幅１００の間にある１の雨粒は５０粒
↓１↓（１）↓１↓（１）↓１↓（１）↓１↓（１）↓１↓ 増加率５０％この理屈は屁理屈でしょうか？本当にこう思うのですが、どなたか正しい方向へ導いてください。
-
こまちさんは、水滴1個と1個が併合する様子を丹念に描写していますが、ポイントはそこではありません。
水滴の半径が同じなら1回の衝突よりも3回とか4回のような複数回の衝突の方が半径の増加率は大きいですよね。
衝突は何回も起こるので、重要なのは一定時間に何回衝突するかの回数なのです。
つまり衝突頻度の違いです。水滴の衝突は、落下速度の差によってつくられます。
落下速度は例えば、
半径1μmの水滴の終端速度は0.00003m/s⇒毎秒0.03ミリ
半径10μmの水滴の終端速度は0.003m/s
半径100μmの水滴の終端速度は0.30m/s⇒毎秒30センチ
です。半径1μmの小さな水滴の落下速度は毎秒0.03ミリメートルですから、ほとんど落下することなく空中を漂っているだけで水滴同士が衝突するチャンスが少ないのです。
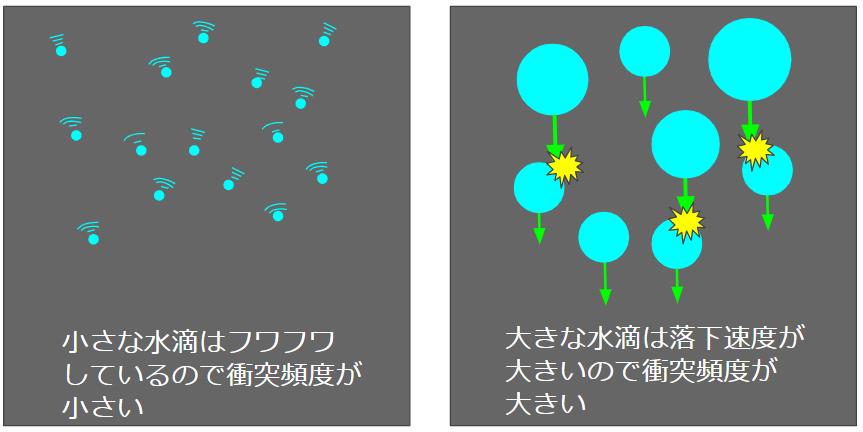
半径100μmの大きな水滴の落下速度は、毎秒30センチメートルですから、僅かな半径の差でも水滴同士の速度差があるので頻繁に衝突します。
この半径増大の模式図は、一般気象学のp86にある図4.5の(b)水滴の併合過程（赤色のライン）で確認することが出来ます。
時間経過とともにラインの傾きが立っているので、半径増加率が大きくなっていることが分かります。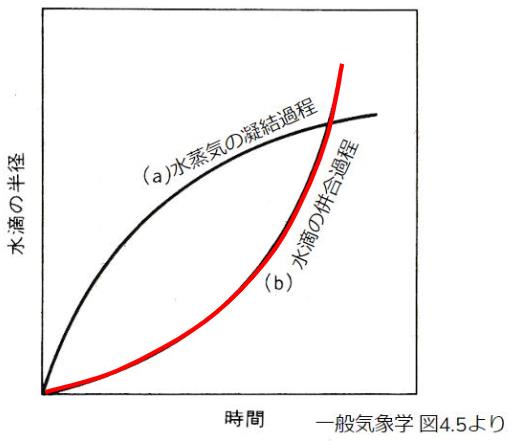
ですから、問題文は誤りです。
『水滴の半径の時間当たりの増加率は、水滴が小さいときには大きいが（小さいが）、水滴が成長するに従って小さくなる（大きくなる）』余談ですが、上図(a)水蒸気の凝結過程では、水滴の半径が大きくなるほど傾きが寝ているので半径増加率は小さくなります。
これは、衝突頻度の変化が小さいので水滴が大きいほど半径増加が小さくなる現象ですから、こまちさんが説明しているイメージに近いのではないでしょうか。 -
水蒸気と水滴は違います。
水蒸気は気体です。
水滴は空中に浮遊していても液体です。
この違いはしっかり認識してください。水滴になって「落下してない」なら理解できますが、
水蒸気が凝結して水滴になった時点で、空気塊の水蒸気量計算からは除外されています。
雲として浮遊していようが、落下しようが空気塊の水蒸気量計算とは関係ありません。仮にΘe:300Kの空気塊があって、雨となって「落下」すれば、この空気塊の含有水蒸気量は減るので、Θeが300Kから下がるのではないのですか？・・・だって、空気塊に含まれてた水蒸気は地表面に落ちてしまってる・・・と解釈しました。
解釈が間違っています。
水滴になった時点ですでに水蒸気ではありませんから、落下しても水蒸気量は減少しません。
相当温位の計算は、すべての水蒸気が凝結した状態を想定して計算します。
湿潤断熱線は、その温度で凝結した水蒸気の潜熱を加味して描かれています。
凝結した水蒸気の潜熱相当分の温位が上昇しているから相当温位は変化しません。
だから、実際に水滴が落下しても、落下しなくても、相当温位は変わりません。こまちさんの間違いは、二つあるように感じました。
・水蒸気（気体）と水滴（液体）を混同していること
・落下した水蒸気だけに注目して、その分の潜熱量と同じ温位上昇を考慮していないこと
です。
-
-
Ｈ２８－１ 問２について
温位は、乾燥空気塊を断熱的に標準大気（ｐ０＝１０００ｈｐａ）まで降下させた時の温度
なお、断熱変化とは、空気塊に外部から熱エネルギーの出入りのない変化(一般気象学P53参照）
相当温位は、飽和している空気塊を断熱的に標準大気（ｐ０＝１０００ｈｐａ）まで降下させた時の温度（一般気象学P67参照）
問文中の「飽和した空気塊が上昇するとき，その温度は湿潤断熱減率に従って低下する。このとき (b) 空気塊の温位は保存する。」は、水蒸気を含む空気が、当該気圧の気温から乾燥断熱線に沿って降下するのでその空気塊はの温位は保存されない。
一方、「飽和した空気塊の上昇に伴って凝結した水分が空気塊から離れて落下すると，(c) 空気塊の相当温位は低下する。」は、同じく水蒸気を含む空気がすべてが凝結（飽和し潜熱を放出）、その点から湿潤断熱線に沿って上昇し乾燥断熱線の交点から降下させた温位。つまり、混合比が０出ない限り常に温位＜相当温位であり、相当温位は保存される。
エマグラムを用いると判りやすいかもしれません。（一般気象学P69）
私の場合、相当温位について、空気塊に含まれる水蒸気を飽和させ雨となり取り除き、水蒸気の持つ潜熱を加味して１０００ｈｐａで比較する温度とイメージしています。また、一般気象学において標準大気（p46）の説明があまり明確ではありませんが、標準大気とは「国際標準大気」のことであり、地球大気の圧力、温度、密度、および粘性が高度によってどのように変化するかを表したモデルのことを差すととに「乾燥空気」であります。現実の大気は、水蒸気を含む「湿潤空気」であることから、気圧、気温の異なるその空気の持つエネルギーを評価するために相当温位という概念があるように解釈しています。Ｈ２８－１ 問４ ｄについて
問文は「水滴同士が衝突し併合して成長する過程では，水滴の半径の単位時間当たりの増加率は，一般に水滴が小さい時には大きいが，水滴が成長するに従って小さくなる。」とあるとおり、併合過程による雨粒の成長についての問いであり、一般気象学P88～92の記載のどおりかと思いますので、参照されてはいかがでしょうか
私の場合、併合過程のポイントとして次のとおり要約解釈しています。
１ ０°Cより高い温度の雲中には水滴を作る凝結核の分布と拡散過程による水滴の成長の違いにより、様々な 大きさの水滴があり、大きさによって水滴の落下速度が異なる。
２ 大きな水滴は落下速度が大きく、落下途中で小さな水滴に衝突し、水滴まわりに付着し成長する。
３ 水滴の大きさが大きいほど、小さな水滴に衝突しやすい。
４ 落下速度がさらに増し、断面積も大きくなる。いっそう他の水滴と衝突しやすくなり、加速度的に成長する。 -
その２の問題は、小粒子が一様に分散している空間内の大粒子の鉛直方向の落下問題として考えます。
半径１の粒子が空間を落下し単位時間に半径0.5の小粒子56個を併合すると、半径は2.0倍になります【1^3+56*0.5^3=8, 8^(1/3)=2.0】。半径2の粒子は落下速度が半径の2乗に比例するとすると4倍の速度で落下するので、単位時間に56個*4倍の224個の小粒子と出会うと思いきや、断面積が4倍になっているのでさらに4倍の896個の小粒子を単位時間に併合します。従って半径は、4.9倍になります【2^3+896*0.5^3=120, 120^(1/3)=4.9】。増加率は4.9/2＝2.45と2.0倍より大きくなります。 -
温位などで基準となるｐ０＝１０００ｈｐａは”標準大気”ではなく”標準気圧（標準大気圧）”で、国際標準大気とは直接的な関係はありません。念のため。
-
その２の問題は、小粒子が一様に分散している空間内の大粒子の鉛直方向の落下問題として考えます。
半径１の粒子が空間を落下し単位時間に半径0.5の小粒子56個を併合すると、半径は2.0倍になります【1^3+56*0.5^3=8, 8^(1/3)=2.0】。半径2の粒子は落下速度が半径の2乗に比例するとすると4倍の速度で落下するので、単位時間に56個*4倍の224個の小粒子と出会うと思いきや、断面積が4倍になっているのでさらに4倍の896個の小粒子を単位時間に併合します。従って半径は、4.9倍になります【2^3+896*0.5^3=120, 120^(1/3)=4.9】。増加率は4.9/2＝2.45と2.0倍より大きくなります。 -
その２の問題は、小粒子が一様に分散している空間内の大粒子の鉛直方向の落下問題として考えます。
半径１の粒子が空間を落下し単位時間に半径0.5の小粒子56個を併合すると、半径は2.0倍になります[1^3+56*0.5^3=8, 8^0.33=2.0] 。半径2の粒子は落下速度が半径の2乗に比例するとすると4倍の速度で落下するので、単位時間に56個*4倍の224個の小粒子と出会うと思いきや、断面積が4倍になっているのでさらに4倍の896個の小粒子を単位時間に併合します。従って半径は、4.9倍になります[2^3+896*0.5^3=120, 120^0.33=4.9] 。増加率は4.9/2＝2.45と2.0倍より大きくなります。 -
おお、これは、失礼しました。
ｐ０＝１０００ｈｐａは、あくまでも温位、相当温位での基準の気圧であり、標準大気ではありません。
国際標準大気についての記載は無視してください。
誤解させてすみません。 -
訂正
「半径は、4.9倍になります」–＞「半径は、4.9になります」
-
